TensorFlow, machine learning I: Perceptrón multicapa

Esta entrada presupone, por parte del lector, ciertos conocimientos de redes neuronales artificiales. No obstante ofrezco una descripción teórica muy rápida.

Las redes neuronales artificiales se basan en el funcionamiento de las redes formadas por células de los sistemas nerviosos cuya principal capacidad es la de excitarse eléctricamente según una serie de estímulos.

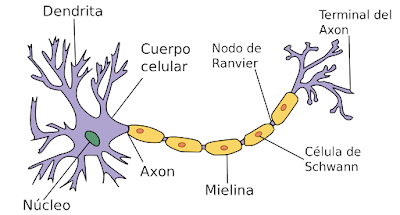
Los estímulos son recibidos a través de las dentritas  y en función de estas entradas la neurona puede activarse y mandar estímulos a través de los axones terminales a otras neuronas o no activarse. Poniendo un ejemplo muy sencillo; supongamos que tenemos una red neuronal encargada de mandar la señal a los músculos para encestar una bola de papel en una papelera; las entradas a las neuronas podría ser al ángulo de lanzamiento y la fuerza, las redes se activan o no según una función de activación determinada que tiene como entrada el valor de las entradas multiplicadas por unos pesos -inicialmente aleatorios-. Este proceso de activación pasará por diferentes capas neuronales, cada una con su función de activación y sus pesos. Finalmente la capa de salida da un valor que se interpreta para colocar el brazo y lanzar. A continuación se observa el resultado y se corrige los pesos usando como criterio la minimización del error -por ejemplo según mínimos cuadrados-. El proceso de lanzamiento-evaluación del error-modificación de pesos-lanzamiento continua hasta que se alcanza el error deseado, a continuación se fijan esos pesos "ganadores". A partir de ese momento lanzar y encestar -en esas mismas condiciones- no debería requerir más entrenamiento, usando siempre los mismos pesos. Evidentemente esto es una simplificación muy grande pero es justo la idea que subyace en las redes neuronales artificiales.

Una vez establecidas estas pequeñas ideas teóricas vamos a implementar una red neuronal  en TensorFlow. Básicamente esto consiste en realizar el siguiente esquema:

 

Por sencillez vamos a usar solo una capa oculta, un solo atributo de entrada y una sola salida. Ampliar a más capas, a más entradas o más salidas es inmediato. 

Básicamente lo que tenemos que hacer es:

1. Establecer el número de entradas.
2. Definir cuantas capas ocultas -hidden layers- que deseamos y cuantas neuronas por capa.
3. Cuales será los pesos iniciales -W-.
4. Añadir el bias.
5. Cual será la función de activación de cada capa.
6. Definir la capa de salida. 
7. Cual será el criterio de error.
8. Entrenar la red.
 

A continuación el código que realiza todo este trabajo:

def neural_net(input_x, output_y, total_epoch):
    x = ts.placeholder("float", [None, 1])
    y = ts.placeholder("float", [None])
    batch_size = 10
    n_input = 1
    n_output = 1
    n_hidden_layer = 10
    w_layer1 = ts.Variable(ts.random_normal([n_input, n_hidden_layer]))
    bias = ts.Variable(ts.random_normal([n_hidden_layer]))
    hidden_layer = ts.nn.sigmoid(ts.add(ts.matmul(x, w_layer1), bias))
    w_layer2 = ts.Variable(ts.random_normal([n_hidden_layer, n_output]))
    bias_out = ts.Variable(ts.random_normal([n_output]))
    output_layer = ts.matmul(hidden_layer, w_layer2) + bias_out

    cost = ts.reduce_mean(ts.square(output_layer-y))
    optimizer = ts.train.AdamOptimizer(learning_rate=0.001).minimize(cost)

    with ts.Session() as sess:
        sess.run(ts.global_variables_initializer())
        for epoch in range(total_epoch):
            error = 0
            total_batch = int(len(input_x) / batch_size)
            for i in range(total_batch - 1):
                batch_x = input_x[i * batch_size:(i + 1) * batch_size]
                batch_y = output_y[i * batch_size:(i + 1) * batch_size]
                feed_dict = {x: batch_x, y: batch_y}
                _, c, p = sess.run([optimizer, cost, output_layer], feed_dict=feed_dict)
                error += c/total_batch
        print("Training finalizado")


x = [[x/100] for x in range(-20, 20)]
y = [y[0]*y[0] for y in x]
neural_net(x, y, 200)

Y ahora una explicación más detallada.

1. Establecer el número de entradas

Esto es establecer cuantos atributos tendremos. En un ejemplo muy sencillo, para hacer regresión de una función desconocida $f(x)$, solo tendremos una entrada.
Otro aspecto importante es crear un placeholter para las entradas y las salidas.  Los placeholter son variables vacías que serán alimentadas más adelante. Si no se alimentan, cuando ejecutemos el algoritmo nos dará un error. Hay que tener en cuenta que si empleáramos Variables en lugar de placeholder los valores podrían ser sobrescritos, de esta forma aseguramos que los valores de entrada y salida para entrenamiento permanecen constantes a lo largo del entrenamiento. Es cierto que también podrían usarse constantes en vez de estas estructuras, sin embargo TensorFlow penaliza este uso limitando el tamaño de las constantes -2 Gb- .Por otro lado los placeholder pueden aumentar dinámicamente el tamaño de la memoria, lo que permite más flexibilidad a la hora de nutrir un modelo con diferentes conjuntos de entrenamiento.

x = ts.placeholder("float", [None, 1])
y = ts.placeholder("float", [None])

En este caso  las entradas se han representado como una matriz de una columna, mientras que la salida está representada por un array.
 

2. Definir cuantas capas ocultas que deseamos y las neuronas por capa

Por lo general no es necesario emplear más de dos capas ocultas, evidentemente hay una razón para ello. Por una lado hay que tener en cuenta que al añadir capas ocultas incrementamos el número de pesos, si la capa anterior tiene m neuronas -o si es la capa de entrada, m entradas- y la nueva capa oculta aporta n neuronas, tendremos en total mxn nuevos pesos. El exceso de pesos puede generar un problema de sobre aprendizaje siendo capaz de aprender "de memoria"  acomodando los pesos para cumplir con unas salidas dentro del error solicitado. El problema es que ante cualquier modificación de las condiciones no es capaz de ofrecer respuestas satisfactorias. Por otro lado el aumento de neuronas implica tiempos de cálculo crecientes. Lo más adecuado es empezar con una sola capa, ir aumentando las neuronas de esa capa esperando que el error se ajuste a lo solicitado. Si los resultados no mejoran entonces habría que pensar en el aumento de capas ocultas. Esto lo definiremos como una contante:

n_hidden_layer = 10

3. Cuales será los pesos iniciales, W. 

Como puede verse cada entrada, o cada neurona, aporta a la activación de todas las que tiene por delante según un peso. Inicialmente estos pesos son aleatorios. 

w_layer = ts.Variable(ts.random_normal([n_input,n_hidden_layer])) 

Esto nos da una matriz de pesos que une cada entrada -una en este caso- con cada una de las neuronas de la primera capa -10-.

4. Establecer el bias.

Cada entrada se multiplica con el peso que le corresponde para cada neurona -tal y como se muestra en el esquema-. Es decir, si tuviésemos 3 entradas $x_{0}, x_{1}, x_{2}$ la entrada a la primera neurona seria $x_{0}*w_{0,0}+x_{1}*w_{1,0}+x_{2}*w_{2,0}$, de igual manera para el resto de las neuronas. Sin embargo resulta conveniente añadir un grado de libertad más al conjunto (un bias), de tal forma que la entrada a la primera neurona de la capa oculta quede como:

$x_{0}*w_{0,0}+x_{1}*w_{1,0}+x_{2}*w_{2,0}+bias_{0}$

En nuestro caso como solo hay una entrada tendremos:

$x_{0}*w_{0,0}+bias_{0}$

El bias fue introducido en el modelo de red Adalina -ADAptative LInear Neuron- por Widrow y Ho (1960).

En nuestro caso el bias para la primera capa oculta lo calculamos como:

bias = ts.Variable(ts.random_normal([n_hidden_layer]))

5. Cual será la función de activación de cada capa.

Lo recibido por cada neurona es procesado por esta y activa la salida en función de la llamada función de activación $f(x_{0}*w_{0,0}+bias_{0})$. Existen diferentes funciones de activación:

• Neurona todo/nada. Representada por una función escalón con un umbral -salida digital-.
• Neurona continua tipo sigmoide.

Hay algunas otras funciones de activación pero estas son las más empleadas. En cualquier caso es necesario que sean derivables como exige el algoritmo de retropropagación del error. El módulo nn de TensorFlow nos proporciona un buen número de funciones de activación. En nuestro caso emplearemos la función sigmoide para calcular la salida de las neuronas de la capa oculta, que no es más que la suma de las entradas pasadas por la función de activación:

hidden_layer = ts.nn.sigmoid(ts.add(ts.matmul(input_x, w_layer), bias))

Esto último requiere una pequeña explicación, aunque realmente no es más que cálculo matricial simple. En cualquier caso tenemos:

  

ts.matmul(input_x, w_layer) -> Producto matricial de la matriz de 

entradas por la matriz de los pesos, si recordamos el producto 

matricial reconoceremos que el resultado es la suma de los productos

de las entradas por los pesos correspondientes, cada fila es justo 

la entrada a cada neurona de la capa oculta.  

 
ts.addts.matmul(input_x, w_layer), bias)) ->  Le sumamos a la matriz anterior los bias. 

6. Definir la capa de salida 

De igual manera debemos establecer lo que llega a la salida desde las neuronas de la última capa oculta -en este caso coincide también con la primera oculta-. Esto se hace con el mismo razonamiento que empleamos en el paso 5. 

w_layer2 =  ts.Variable(ts.random_normal([n_hidden_layer, n_output]))
bias_out = ts.Variable(ts.random_normal([n_output]))
output_layer = ts.matmul(hidden_layer, w_layer2) + bias_out

6. Cual será el criterio de error y el algoritmo de optimización

El aprendizaje de una red neuronal es de tipo supervisado, esto significa que deberemos disponer de un conjunto de datos con sus entradas y con sus salidas correctas, de tal manera que la propia red sepa en que medida su predicción es la adecuada, corrigiendo los pesos para mejorar su predicción. Para ello debemos dar a la red un criterio para establecer lo bien que esta realizando su tarea. La función de error cumple precisamente este cometido, también llamada función coste.

cost = ts.reduce_mean(ts.square(output_layer-y)

Como puede observarse esto no es más que el error cuadrático medio. 

Una vez establecido el error a estimar hay que decidir como buscar el mínimo. Cambiar los pesos sin criterio, al zar, no es un método efectivo para minimizar una función de coste. Entre los muchos métodos que se pueden elegir, uno muy efectivo es el de descenso de gradiente. De forma muy resumida, dada una función F que queremos minimizar, probablemente $F(x_{n+1})<F(x_{n})$ para:

$x_{n+1}=x_{n}-\gamma \bigtriangledown F(x_{n})$

El método de descenso de gradiente Adaptive Moment Estimation o Adam es una implementación más efectiva del descenso de gradiente: 

optimizer = ts.train.AdamOptimizer(learning_rate=0.001).minimize(cost)

7. Entrenar la red

Una vez configurada la red debemos empezar el entrenamiento. Básicamente esa tarea se realiza en el siguiente código: